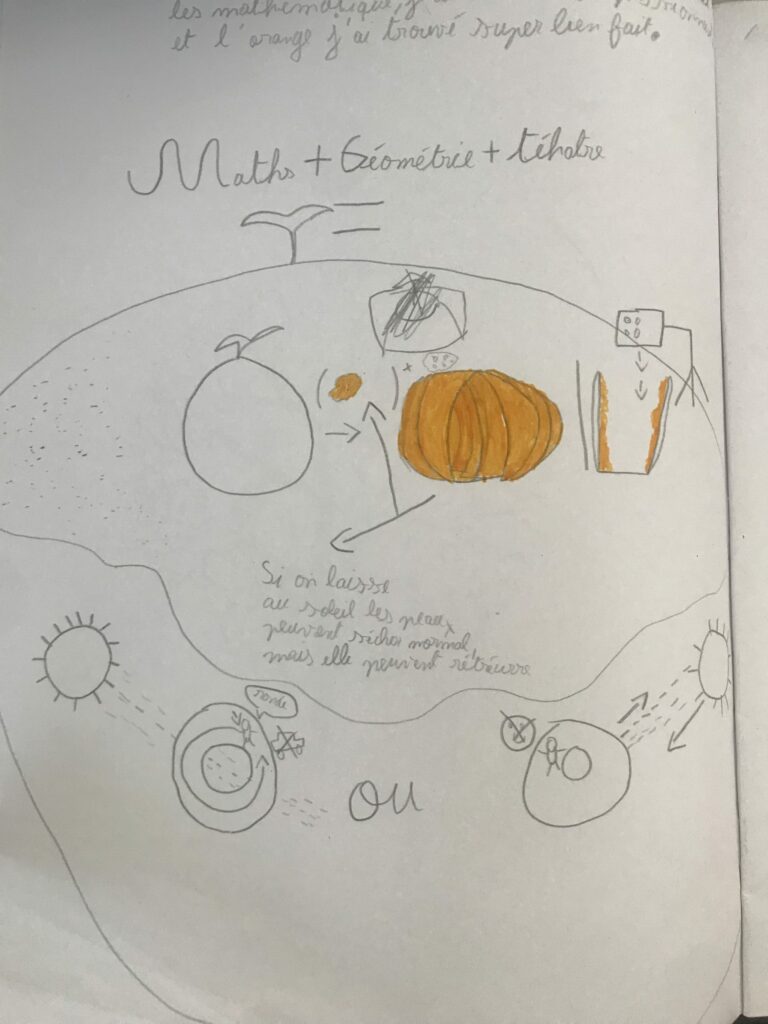
La terre est bleue comme une orange
CARNET DE BORD
— avril 2023 Nantes
restitution de l’expérimentation au Laboratoire de Mathématiques Jean Leray à l’Université de Nantes
Katerini Antonakaki en jeu et Baptiste Chantraine en regard
un grand merci aux chercheurs qui ont participé à l’expérience
à suivre ….

— avril 2023 Saint Nazaire
restitution de l’expérimentation à Athénor scène nomade CNCM
Katerini Antonakaki en jeu et Baptiste Chantraine en regard
ouverture au public et aux élèves des ateliers qui ont présenté une petite forme théâtrale autour du projet et assisté à la restitution du carnet de bord performatif de l’expérimentation

— avril 2023 Angers
atelier images et mise en place de la restitution
Katerini Antonakaki et Olivier Guillemain
O le point dimension zéro / immobilité + la ligne dimension 1 / mouvement
OR le plan dimension 2 – dehors, hors bord, alors / voyage
A la sphère
AN en grec si si et seulement si dans l’orange il n’y avait pas d’orange / dimension 3
NE jamais croire que c’est vrai sans vérifier / auscultation d’orange
ANGE un ange passe / il y a quelqu’un ?
RANGE RAGE ORAGE
la lumière qui arrive dans ton œil transporte les fragments de l’objet que tu regardes
ORANGE
l’objet devient de plus en plus gros jusqu’à t’envahir complètement

— mars 2023 Nantes
Retour sur quelques points de la recherche.
Katerini Antonakaki et Baptiste Chantraine
Il y a plusieurs infinis. Et tout ce qu’on ne sait pas encore que l’on ne sait pas.
Le point de vue, les temps de réflexion, les calculs entre la pensée et les dessins au tableau.
On devrait être capable d’’expliquer un problème de géométrie sans dessin, sans dire ça, ici, tu vois ?
La question de la mise en forme, du langage et même du contenu, de ce qui sera l’objet scénique de notre expérimentation, plane par moment dans la salle au tableau vert, en résonance aux coup de craie vifs et doux à la fois, rythmés par une géométrie en roue libre vers des espaces passionnants sortis juste d’un fruit bleu orange.

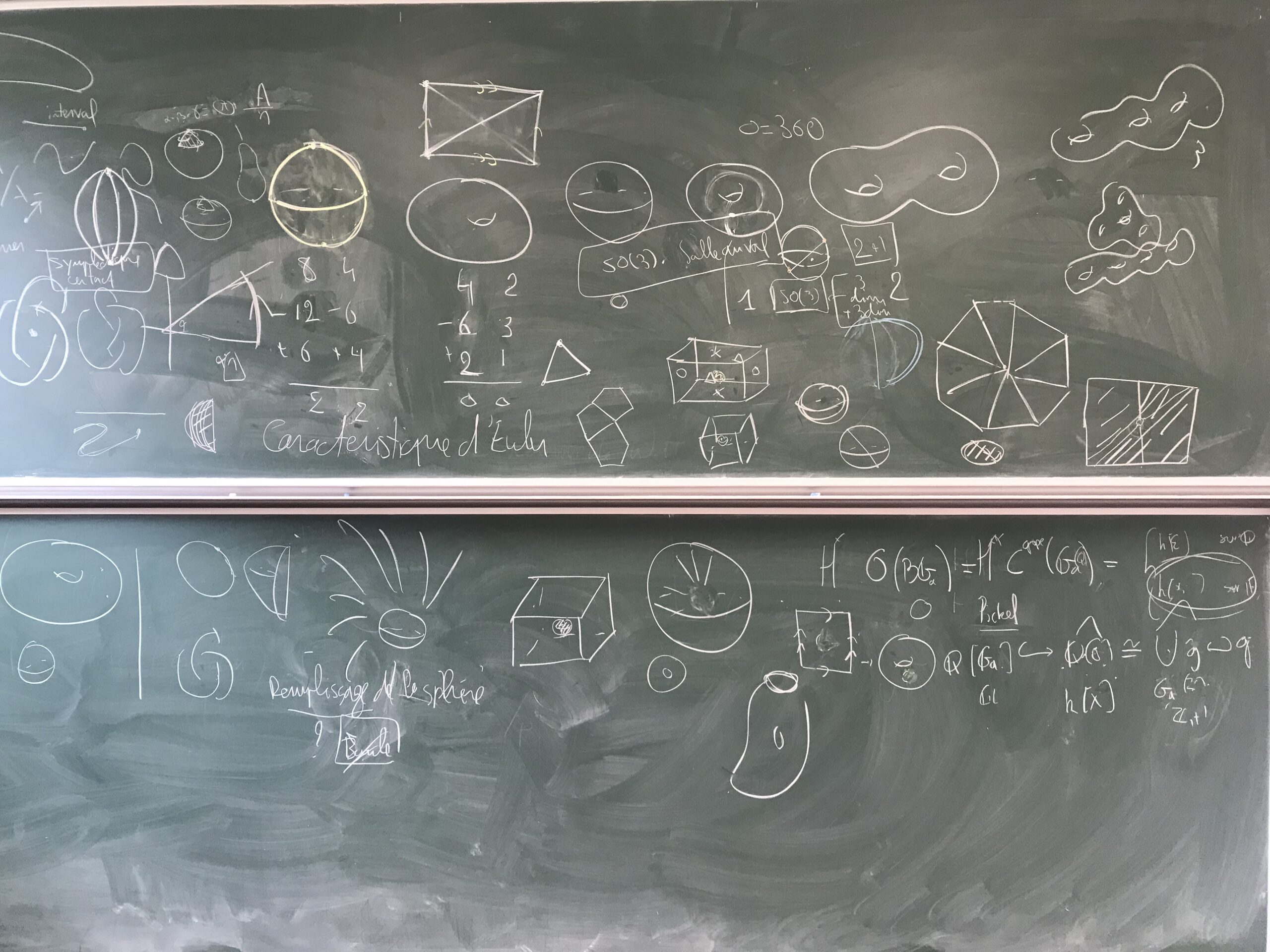
— février 2023 Saint Nazaire
Atelier autour du projet, mis en place par Athénor scène nomade CNCM, avec deux classes de l’Ecole Jules Simon
Katerini Antonakaki et Baptiste Chantraine à distance
accompagnés de Fréderic Bechet
Caractéristique de l’Euler. F – E + V = 2
Expérience en classe par groupe de trois. Sur la surface d’une orange planter des piquets, relier avec des fils. Compter les faces (F), les côtés (E) et les points (V). Appliquer la formule. Sur la sphère on obtient toujours 2.
Notes sur l’observation du processus.


— février 2023 Amiens
Laboratoire sonore – esquisse de programmation sur le casque acoustique 8 pistes en construction
Katerini Antonakaki et Christine Moreau
Imaginer que nous sommes assis la tête à l’intérieur d’une orange. Que cette orange contient un espace de dimension 3 avec la possibilité de se déplacer un avant, en arrière, à droite, à gauche, en haut et en bas. Déjà ça. Créer l’expérience sonore pour expérimenter les sensations.
Ou alors. Imaginer que dans l’orange nous sommes dans une dimension n+3 ? et dans ce cas la quatrième dimension du temps apparaît, avec l’avant et l’après en plus des autres directions. Dans ce cas, le son qui entre dans l’orange ne sortira pas forcément par le côté opposé mais rebondira sur les parois jusqu’à trouver le bon angle de sortie. Créer l’expérience sonore pour expérimenter les sensations.

— janvier 2023 Nantes
Interrogations
sur un hypothétique intérieur d’orange contenant un tore.
Katerini Antonakaki et Baptiste Chantraine
Les huit géométries.
Une dimension est une information. Le référentiel.
On rend le réel abstrait. Face à quelque chose que l’on ne peut résoudre, on prend un autre exemple.
Le bord de l’orange. L’angle. La somme des angles sur un espace. Le point de vue. L’infini.
Prototype sur la caractéristique de l’Euler – découpage d’une sphère en triangles.

— novembre 2022 Saint Nazaire
Atelier autour du projet, mis en place par Athénor scène nomade CNCM, avec deux classes de l’Ecole Jules Simon
Katerini Antonakaki et Baptiste Chantraine
accompagnés de Fréderic Bechet
Est-ce que je dois connaître l’orange avant de l’étudier ?
Mathématiques – un langage pas comme les autres.
Que veut dire différent ?
L’orange n’est pas bleue. Et la Terre ?
Les analogies. Le décalage. Les indices.
Il faut marcher. La sphère est le bord de la boule.
Même si on connaît la réponse, la question développe l’imagination.
L’approximation un outils fascinant.

— novembre 2022 Nantes
Géométrie de l’orange
Katerini Antonakaki et Baptiste Chantraine
Qu’est-ce qui définit un objet ?
Rien n’est exactement comme on l’imagine.
La perception et la dite réalité se confrontent et cohabitent. Chaque question est une piste de décollage – connectique du cerveau vers l’imagination. Ce qui nous intéresse n’est pas vraiment nommable.
La mémoire des 5 sens est une base de données précieuse – la connexion avec l’orange reste intime : son goût, son odeur, sa forme et sa couleur, ses différentes couches et surfaces et pour l’ouïe la mémoire des sons des orangeraies.
Au départ une question. L’orange. Qu’est-ce qu’il y a dedans ? Imaginer être tout petit à l’intérieur.
Les dimensions. Le point comme base pour fabriquer des espaces. Le point attaché sur quelque chose. La feuille de papier. Le tore.
L’élasticité ou alors les distances. Topologie, une autre Géométrie. Toute chose est différente. La théorie des ensembles.
Les trajets qui reviennent au même point. Tout doit aller quelque part et en une fois. Le bord du bord. Creuser un trou. Les hypothèses. On suppose, on accepte et on observe ce qu’on obtient.
Isoler l’horizon. Juste un trait de surface.
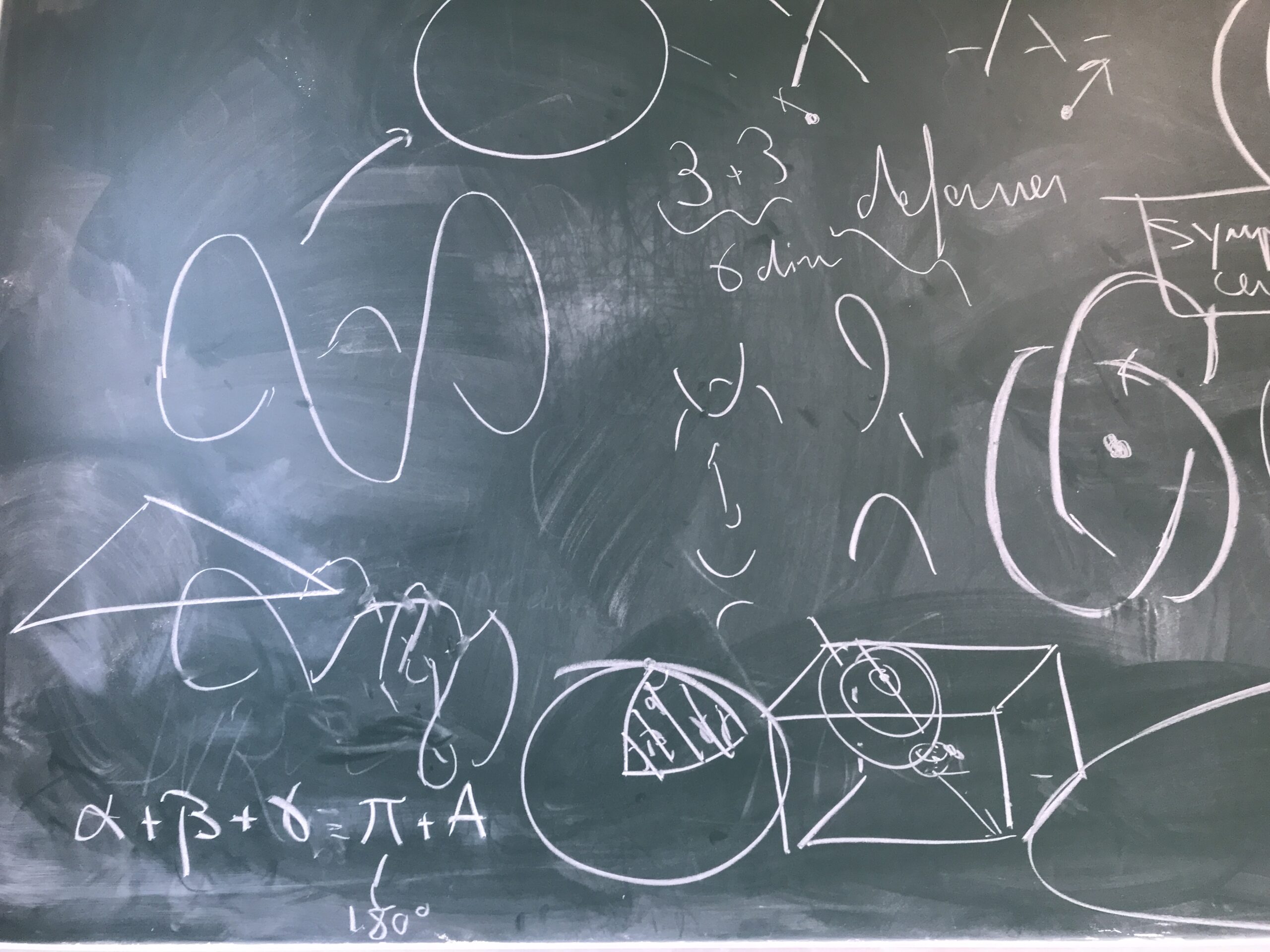


— octobre 2022 Annecy
Laboratoire sonore
Katerini Antonakaki et Christine Moreau
En studio improvisé et en promenade au bord du lac, l’orange a été mis en situation dans des contextes différents. En essayant d’enregistrer le contact de sa surface avec différentes matières nous avons récolter des sons et des réflexions sur les possibles interactions entre les paysages sonores à inventer et les expérimentations visuelles à venir. Aucune des expériences non destructibles n’a pu prouver que dans l’orange se trouver bien une orange.


— octobre 2022 Nantes
Trois jours de géométrie topologique
Katerini Antonakaki et Baptiste Chantraine
L’orange continue à nous intriguer cette fois avec la complicité de quelques chercheurs en Géométrie du Laboratoire de Mathématiques Jean Leray à l’Université de Nantes.
Les questions nous guident. La sphère révèle ses lois et la surface de l’orange est scrutée par des fourmis géomètres improbables. Et si dans l’orange se cachait un espace à plus que 3 dimensions? Les mathématiciens remplissent l’intérieur du fruit avec des formules, croquis, hypothèses et autres paroles – haut potentiel de création dessiné pas à pas au tableau. Paysages de la pensée qui défilent et s’entrelacent pour notre plus grand enchantement.
Merci aussi à Athénor – scène nomade CNCM pour cette mise en relation – rencontre enivrante à suivre tout le long de la saison.
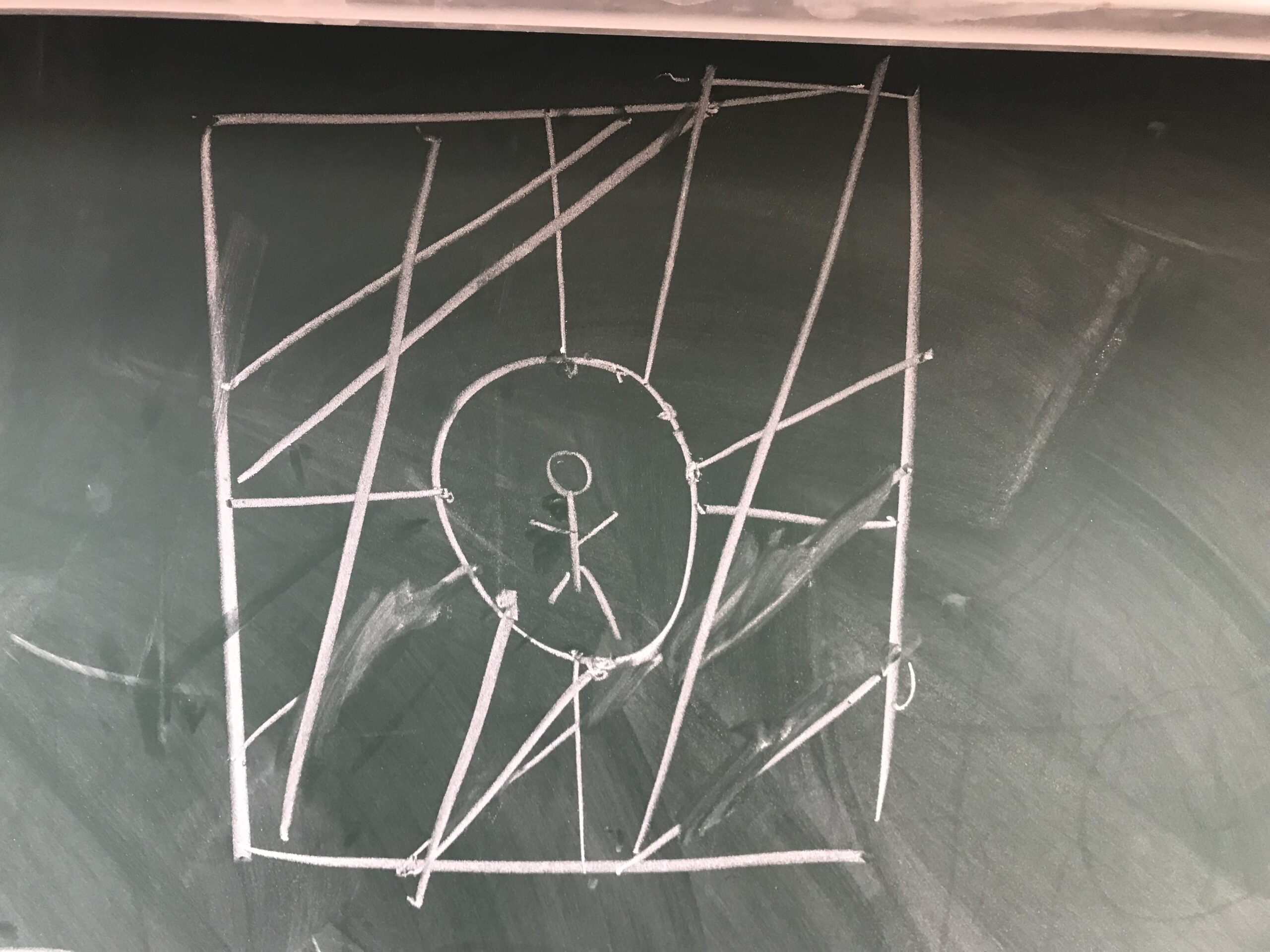

— août 2022 Angers
Semaine d’expérimentation avec la matière.
Katerini Antonakaki et Olivier Guillemain
Nous avons découpé, épluché, pressé, gratté, givré, goûté, enflammé puis fait tourner, rouler, tomber, puis tout a séché n’importe comment alors nous avons épinglé, scotché, cousu, filmé, scanné et surtout observer attentivement onze oranges qui se sont portées volontaires.
Potentiel élevé pour les prochaines sessions. Grandes interrogations sur nos objectifs de départ. Première intuition : ne pas chercher à montrer ni savoir ce que réellement se trouve dans l’orange, mais plutôt essayer de déduire et imaginer ce que possiblement constitue ce fruit-planète qui nous nargue.

— 4 juillet 2022 Nantes
Rencontre de Katerini Antonakaki avec le mathématicien Baptiste Chantraine du Laboratoire de mathématiques Jean Leray.
Une mise en bouche du projet d’expérimentation accompagné par Athénor scène nomade CNCM.
Accepter de ne pas comprendre.
En plein été l’orange ressemble à un souvenir lointain qu’on a du mal à cerner.
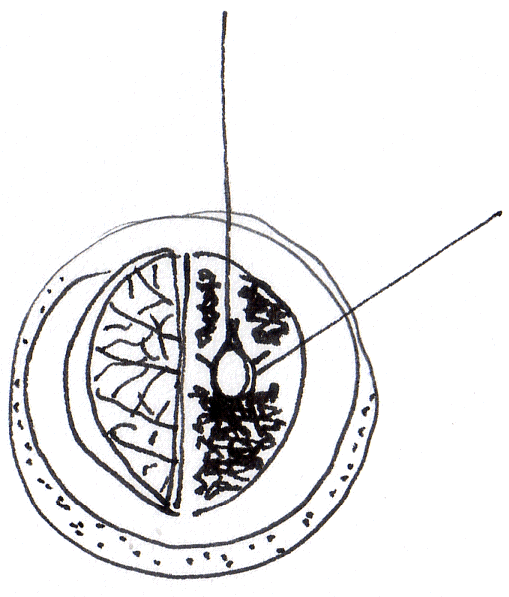
Quelques mots simples mêlés à des théorèmes géométriques – dessins graphiques et calculs improbables à inventer.
Approche topologique des cinq sens.
En tout cas l’abstraction semble au beau fixe.

orange … range ronge rage orage âge or orge ogre ange nage gare organe onagre et aussi gré géo néo …
… il y a dans l’orange une aspiration à reprendre contenance après avoir subi l’épreuve de l’expression…
Francis Ponge – Le parti pris des choses

— 1er mai 2022
Notes sur les possibles liens du projet avec les mathématiques
Quelques portes d’entrée :
– étudier l’orange comme un monde régi par des lois plus ou moins simples. Il doit y avoir des formules mathématiques pour définir un monde parfaitement stable, à moins que ce fruit soit déjà un système chaotique à lui seul.
– étudier sa composition, vers une modélisation de ses strates d’aspects différents, pour évaluer la trajectoire de nos outils en vue d’une intrusion d’exploration à l’intérieur du fruit.
– décrypter les formules mathématiques qui expliquent ou anticipent les phases de l’expérience
– rester ouverts à toute déviation qui apparaîtra comme une nouvelle piste d’exploration
Même si la recherche ne se précisera que sur le chemin, nous aimerions pouvoir cerner plus concrètement la proposition, pour l’instant instinctive et non scientifique, avec l’aide des chercheurs mathématiciens.
La terminologie très évocatrice convoque la réflexion philosophique et poétique qui se met en route dès qu’on effleure certains chapitres.
Voici déjà quelques exemples :
La théorie du chaos
l’orange et ses propriétés
L’effet papillon
l’intrusion et ce que cela provoque dans la composition du fruit
Le hasard et les événements aléatoires
probabilités d’écart entre l’énoncé de la recherche et la réalité de l’expérimentation
La théorie des systèmes dynamiques
étude de la trajectoire des nos outils d’exploration
Les attracteurs étranges ou chaotiques
observation et traduction mathématique du moment de la transition vers le chaos
Les figures fractales ou catastrophes
modélisation de quelques parties du fruit – de la formule vers l’image
La théorie des bifurcations
suivi mathématique de nos explorations
La topologie géométrique – la théorie de la chirurgie
propositions mathématiques à réaliser avec les objets en vrai
Et il y a aussi, pour le carnet de bord et l’énoncé du problème, la géométrie euclidienne avec les formules de calcul pour les volumes à explorer et, en plus complexe, la géométrie différentielle, avec le potentiel de jauge et la déviation d’un champ de vecteur, qui utilisent des dessins très expressifs.